Questão: Como adicionar mais informação às instruções?
Até agora, o nosso computador possui as seguintes limitações:
Permite a entrada de dados somente através das chaves;
Não possui memória além do registrador interno (falta memória externa);
Não acessa periféricos outros que as chaves e os LEDs de saída;
Não suporta a utilização de constantes definidas dentro do programa;
Não possui mecanismo de desvio na execução do programa.
Essas limitações serão resolvidas através de uma reorganização do formato das instruções, do nosso computador, que permita uma maior versatilidade na utilização de operandos.
Como exemplo, vamos analisar a execução da seguinte operação: A = B + 8. Atualmente, as constantes e variáveis devem ser obtidas através das chaves e armazenadas no acumulador (registrador A) ou entrando diretamente na entrada B da ULA. Não temos uma instrução que tenha uma constante definida internamente ou mesmo uma instrução que faça acesso à uma memória externa - que poderia ser utilizada como rascunho.
Isso é devido ao formato da instrução que, atualmente, possui somente o opcode (código da operação a ser executada). Uma forma mais genérica seria uma instrução que tivesse um campo para o opcode e um, ou mais, campos para os operandos necessários.
Para resolver A = B + 8, considerando que as variáveis estão em uma memória externa (chamada M) e que a constante está embutida na instrução, poderíamos ter o seguinte código:
LDI 8 # Carrega Acumulador com 8
SOMA M[enderecoVariavelB] # Soma Acumulador com Variável B
STA M[enderecoVariavelA] # Armazena resultado na posição de memória da Variável AOnde: M = Memória externa; SOMA = soma acumulador com conteúdo da posição de memória; LDI = Load Imediato: operação de carga de uma constante (definida dentro do campo da instrução); STA = Store Acumulador: operação de armazenamento em posição de memória
A instrução LDI, que carrega o acumulador com uma constante, precisaria de uma organização do tipo:
| opCode | Constante Embutida na Instrução | |
|---|---|---|
| X bits | K bits |
No caso, o valor X é o número de bits necessário para codificar todas as instruções existentes no processador. O valor K é o número de bits necessário para representar a faixa de valores utilizados para constantes.
Porém, a instrução LDI precisa que o valor contido no campo imediato da instrução passe pela ULA e vá para o acumulador. Isso necessita de uma nova operação na ULA, em que a saída da ULA será o valor da entrada B da ULA. Para poder selecionar essa função na ULA, precisaremos de mais um bit no ponto de controle da operação.
A instrução STA, que salva o valor do acumulador em uma posição de memória, teria uma organização do tipo:
| opCode | Endereço de Memória | |
|---|---|---|
| X bits | Y bits |
Novamente, o valor X é o número de bits necessário para codificar todas as instruções existentes no processador. Já o valor Y é o número de bits necessário para endereçar todas as posições de memória e periféricos que existem no computador.
A instrução LDA (carrega um valor de memória para o acumulador), que é simétrica à instrução STA, teria uma organização igual à da STA. Porém, a instrução LDA, de forma similar ao LDI, precisa que o valor contido na memória passe pela ULA e vá para o acumulador. Para tanto, pode usar a mesma operação da ULA utilizado na instrução LDI, em que a saída da ULA será o valor da entrada B da ULA.
A instrução SOMA (soma um valor de memória com o acumulador e armazena no acumulador), funciona de forma similar ao LDA.
No nosso processador, a instrução CLRA pode ser substituída por LDI 0, que carrega o acumulador com o valor zero.
Para que essa modificação funcione, precisamos adicionar, ao nosso processador, um barramento de endereços (para endereçar a memória) e um barramento de dados (para ler ou escrever na memória). O espaço de endereçamento do processador é a quantidade de posições endereçáveis pelos bits (2 elevado ao número de bits) que formam o barramento de endereços. Dessa forma, um barramento de endereços com 8 bits cria um espaço de endereçamento de 256 posições, enquanto um barramento de 16 bits cria um espaço de endereçamento de 65536 posições. Esses endereços podem ser para memória e/ou periféricos, mesmo assim, o espaço total é chamado de espaço de endereçamento de memória.
Isso nos permite transferir a entrada por chaves para uma posição de memória e a saída para os LEDs para outra posição de memória.
Vamos alterar o nosso computador para que ele tenha as seguintes características:
Trabalhar com 8 bits e não mais 4 bits;
opCode de 4 bits (16 instruções possíveis);
Endereçamento de memória com 512 posições (9 bits de endereço), cada uma com 8 bits de dados:
Imediato de 8 bits (pode representar os inteiros de 0 a 255 ou inteiros com sinal de -128 a 127).
Note que o endereço da memória e o valor imediato são utilizados por instruções diferentes. Isso permite que esses campos se sobreponham e seu significado será analisado conforme a instrução decodificada.
No FD acima, a memória está dividida em dois blocos de 256 bytes cada com a seleção feita através da linha de endereçamento A8.
Responder o quiz de participação, no blackboard, em:
Conteúdos > Participação > Aula_4_Quiz-P1
Para adicionar essas funcionalidades, precisaremos definir novos opcodes para as novas instruções. Para tanto, utilizaremos a tabela abaixo:
| Instrução | Mnemônico | Código Binário | Sel MUX | Habilita A | Operação (2 bits) | habLeituraMEM | habEscritaMEM |
|---|---|---|---|---|---|---|---|
| Sem Operação | NOP | 0000 | |||||
| Carrega valor da memória para A | LDA | 0001 | |||||
| Soma A e B e armazena em A | SOMA | 0010 | |||||
| Subtrai B de A e armazena em A | SUB | 0011 | |||||
| Carrega valor imediato para A | LDI | 0100 | |||||
| Salva valor de A para a memória | STA | 0101 |
As saídas que estão indicadas como X ou XX devem ser implementadas como 0 ou 00. Isso facilita o processo de debug do projeto.
Vamos aplicar esse novo formato de instruções ao nosso computador e adicionar/modificar as instruções como visto acima.
Lembre de utilizar a tabela com os pontos de controle, adicionando os novos pontos, para criar as instruções desejadas.
Será necessário alterar o decodificador de instruções para atender a esse novo formato.
Também devemos adicionar uma nova funcionalidada à ULA, chamada de passa: a transferência do valor presente na entrada B para a saída da ULA.
Por fim, vamos implementar o circuito do computador. Para simplificar, vamos utilizar uma versão somente com uma memória, mapeada entre os endereços 256 e 511, como visto na figura abaixo.
Para fazer o programa para resolver a equação S = 3x - 4, precisaremos iniciar as variáveis na memória do computador.
No programa abaixo, consideramos que a variável x vale 3 e está armazenada na posição 256 de memória.
A constante será armazenada na posição 257 de memória.
LDI $4 ; Acumulador = 4
STA @257 ; Armazena 4 na posição 257
LDI $3 ; Acumulador = 3
STA @256 ; Armazena 3 na posição 256
Soma @256 ; Soma acumulador com conteúdo de 256
...O caractere arroba (@) indica um endereço da memória RAM enquanto que o caractere cifrão ($) indica um valor constante (imediato).
Agora, precisamos completar o programa e fazer os testes.
O resultado da compilação será o circuito, em RTL, mostrado no diagrama abaixo.
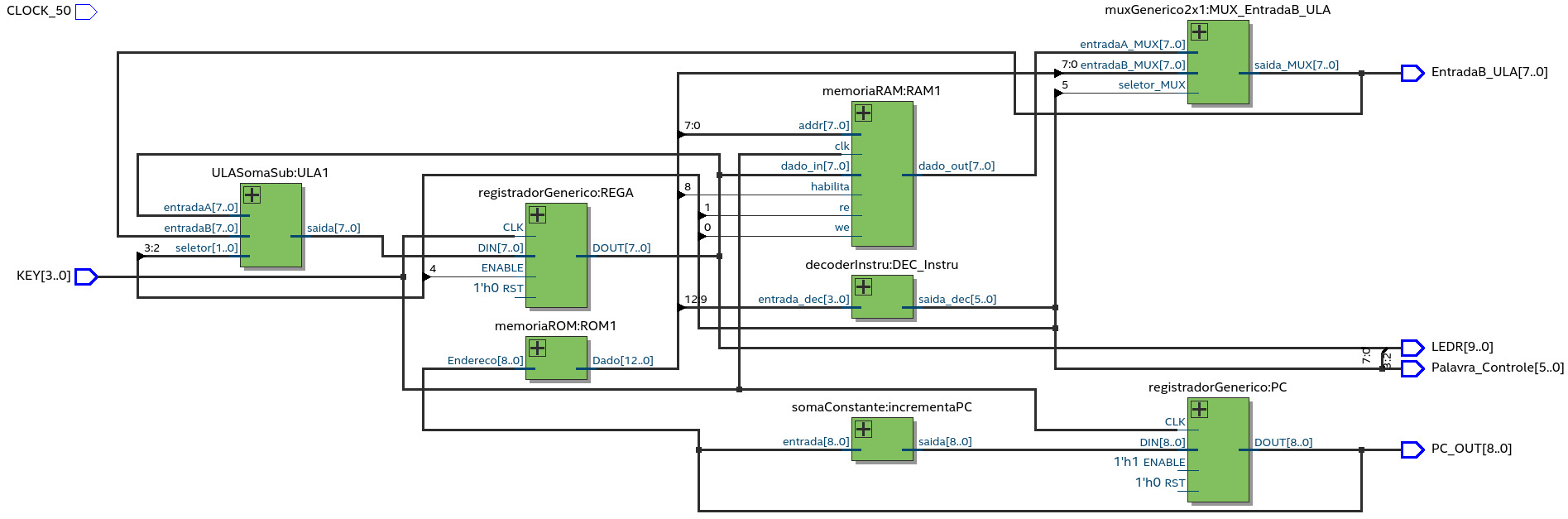
Para fazer a simulação, reagrupe os sinais de entrada e saída conforme o mostrado na figura abaixo.
Além disso, repare nos valores da entrada de dados, mostrados abaixo.
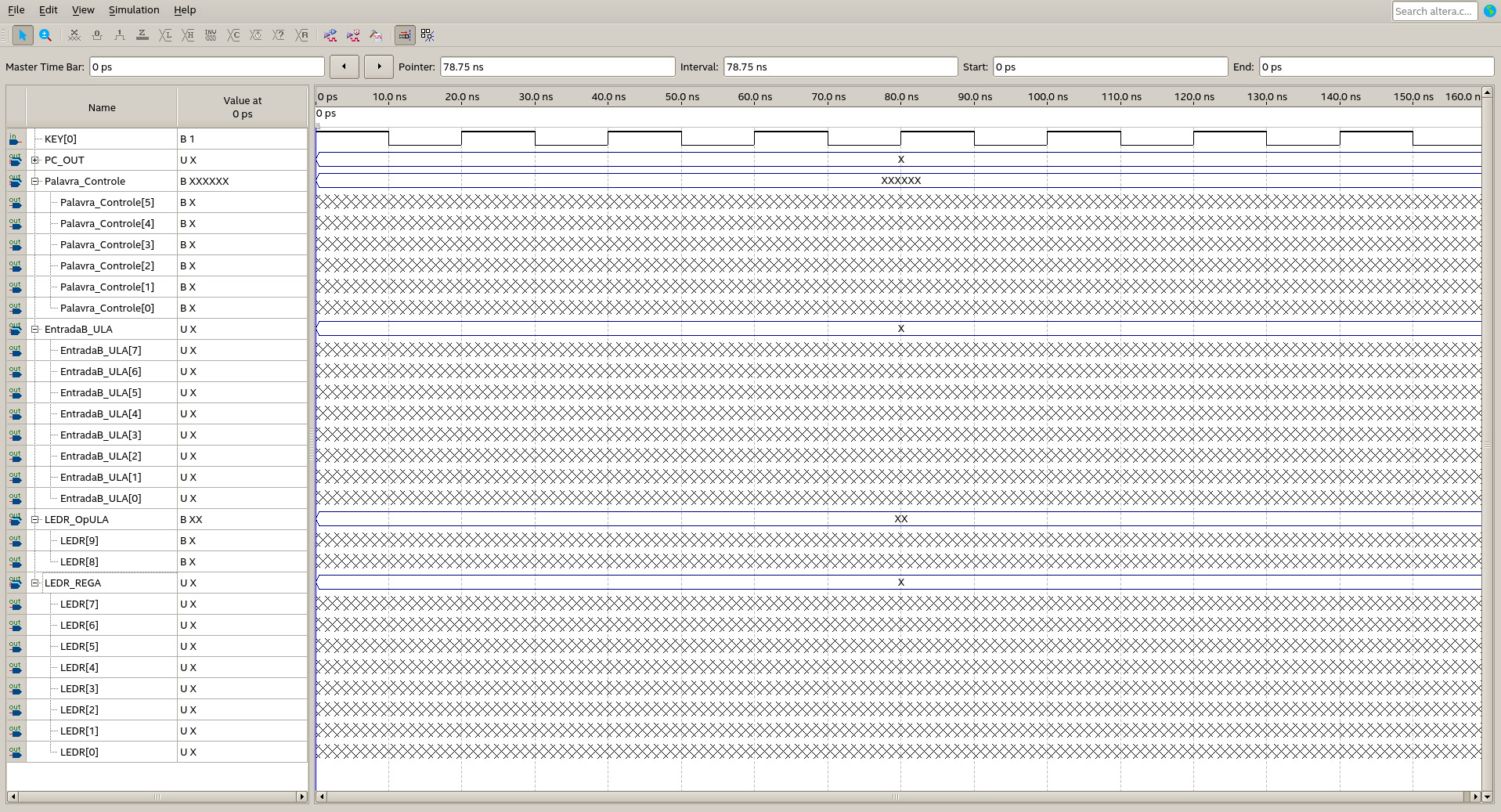
Considerando o valor de X como sendo 3, o resultado da simulação está mostrado abaixo.

Esta Atividade deverá ser entregue através do Blackboard!